PEANO (G.)

PEANO (G.)

Le mathématicien italien Peano s’est principalement intéressé aux fondements des mathématiques, ainsi qu’à la théorie des langages. Grâce à lui, on comprendra mieux aujourd’hui la fécondité des méthodes formelles et axiomatiques. L’actualité de son œuvre ne fait que croître.

Un mathématicien turinois

La carrière universitaire de Giuseppe Peano, né à Cuneo et mort à Turin, s’est entièrement poursuivie dans cette dernière ville. Il y fut étudiant, puis assistant et suppléant du professeur Angelo Genocchi, auquel il succéda à la chaire de calcul infinitésimal. Il conserva cette chaire de 1890 à 1932 et occupa également une chaire à l’Académie militaire de Turin (1886-1901).

De son vivant, sa réputation scientifique n’a jamais été négligeable: cependant, ses préoccupations mathématiques étaient souvent considérées comme marginales et sans véritable avenir. L’attitude d’Henri Poincaré est typique; il écrit dans Science et méthode : «J’ai la plus grande estime pour M. Peano, qui a fait de très jolies choses (par exemple sa courbe qui remplit toute une aire), mais enfin, il n’est allé ni plus loin, ni plus haut, ni plus vite que la plupart des mathématiciens aptères et il aurait pu faire tout aussi bien avec ses jambes.»

La postérité a fait justice de cette sévérité: on trouve Peano à l’origine d’idées tenues de nos jours pour fondamentales.

La critique de l’analyse infinitésimale

Les premiers travaux de Peano sont liés à la rédaction d’un court traité de calcul différentiel et intégral, publié sous la signature de Genocchi (ce dernier a maintes fois déclaré que l’ouvrage était essentiellement dû à son assistant Peano).

Ce remarquable traité contraste avec presque tous les livres similaires de l’époque, où on lisait couramment sous les plumes les plus autorisées des «définitions» telles que: «La différence ou différentielle d’une quantité est l’accroissement ou la diminution instantanée de sa valeur.» Même E. Borel se permet, en 1905, d’écrire: «On appelle dérivée d’une fonction y , ce que devient l’expression du rapport y / x de l’accroissement correspondant de la variable x lorsque, dans ce rapport exprimé au moyen de x et de x , on remplace x par 0.»

Face à ce laxisme, l’auteur s’attache à formuler les concepts sans ambiguïté et à analyser le champ de validité des théorèmes fondamentaux de l’analyse réelle. Il donne souvent la première démonstration correcte d’un énoncé «bien connu». Il a dépisté un grand nombre d’inexactitudes et d’erreurs graves dans les ouvrages de ses prédécesseurs et de ses contemporains. Pour mettre en évidence ces incorrections, Peano se révèle le «maître du contre-exemple». La construction de telles réfutations n’était pas encore entrée dans les mœurs et suscitait même quelques réprobations. Ainsi, Poincaré écrit: «Autrefois, quand on inventait une fonction nouvelle, c’était en vue de quelque but pratique; aujourd’hui, on les invente tout exprès pour mettre en défaut les raisonnements de nos pères et on n’en tirera jamais que cela.»

Citons les analyses de Peano concernant le reste de la formule de Taylor, à une ou plusieurs variables (il découvre le reste de Young, bien avant cet auteur), la théorie des maxima, le théorème des fonctions implicites, etc. Il signale que la paire de fonctions t 料 t ² et t 料 t |t | admet un déterminant wronskien identiquement nul, bien que ces deux fonctions ne soient pas linéairement dépendantes. On doit à Peano la démonstration du théorème d’existence des solutions de l’équation différentielle:

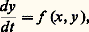où f n’est soumise qu’à l’hypothèse de continuité. Il remarque que cette hypothèse n’assure pas l’unicité locale de la solution. Peano a mis en évidence la distinction entre la continuité partielle et la continuité globale des fonctions de plusieurs variables. Il signale que la fonction f , égale à 0 au point x = 0, y = 0, et à xy /(x ² + y ²) en dehors de l’origine, est partiellement continue sans être continue par rapport à l’ensemble des deux variables. On trouvera d’autres contre-exemples dus à Peano à l’article CALCUL INFINITÉSIMAL – Calcul à plusieurs variables.

Indépendamment de H. A. Schwarz, il souligne les difficultés que comporte la définition de l’aire d’une surface à l’aide d’une suite de polyèdres inscrits. Les deux auteurs proposent le même contre-exemple, la «pomme de pin de Schwarz».

Le joyau le plus célèbre de ces ingénieuses combinaisons est la courbe de Peano qui remplit un carré. Il s’agit de construire une paire (x , y ) de fonctions d’une variable réelle t , de sorte que l’image de l’intervalle [0, 1], par l’application t 料 (x (t ), y (t )), soit un carré de R². La figure ci-contre suggère la construction. Au point de subdivision du segment [0, 1] en 9 parties égales, on associe les 10 points marqués 0, 1, 2, ..., 9. Puis on répète la même construction sur chacun des intervalles de longueur 1/9 obtenus. En poursuivant indéfiniment cette construction, on obtient, par passage à la limite, l’exemple cherché.

La formalisation

La langue usuelle est peu adaptée à la rigueur mathématique. Cela incite Peano (après C. S. Peirce, E. Schröder et G. Frege) à réaliser le vieux projet de Leibniz: l’élaboration d’un langage formalisé, utilisant peu de symboles et soumis à une grammaire rationnelle. Le symbolisme de Peano, qu’il nomme pasigraphie (cf. illustration), sera repris, avec des modifications mineures, par B. Russell et A. Whitehead dans Principia Mathematica . Essentiellement, les mêmes notations sont utilisées de nos jours (cependant, Peano écrit 廬 là où l’on écrit actuellement 歷, face=F3210 履 au lieu de 輦, etc.). Ce n’est pas un langage complètement formalisé, car il comporte de nombreux symboles d’abréviation.

Avec la collaboration de nombreux élèves, Peano rédige de 1894 à 1908 son Formulaire de mathématiques qui préfigure, avec un demi-siècle d’avance, les fascicules de résultats de N. Bourbaki. Il s’agit de réécrire, en langage pasigraphique, les fondements des mathématiques. Le Formulaire traite successivement de logique, des fondements de l’arithmétique, de l’analyse et de la géométrie.

Auparavant, Peano s’intéresse à l’élaboration de symbolismes intrinsèques. En 1888, il publie le Calcul géométrique selon l’Ausdehnungslehre de Grassmann , où s’élabore le calcul vectoriel, compte tenu des travaux de W. R. Hamilton, G. Bellativis, A. F. Möbius... Il faudra plus de trente ans pour imposer le calcul vectoriel dans l’enseignement des mathématiques, et là encore Peano est un précurseur.

L’intérêt de Peano pour les langages rationnels ne se borne cependant pas au seul domaine mathématique. Pionnier du mouvement pour une langue auxiliaire internationale, il fut président de l’Academia pro interlingua. Dans ce domaine, ses travaux comportent l’étude critique des diverses langues proposées (volapük, esperanto, etc.), la compilation du vocabulaire commun aux langues vivantes usuelles, ainsi que l’élaboration du latino sine flexione , qui utilise le vocabulaire latin sans en adopter la grammaire. Les déclinaisons et conjugaisons y sont supprimées, ainsi que les distinctions de genre et de nombre, conformément aux suggestions de Leibniz. Par exemple, on écrit «mater est bono », et, si l’on tient à insister sur le genre féminin de la mère, «mater est femina bono ».

Actuellement, la linguistique a pris une importance de premier plan. Là encore, Peano est à l’origine du mouvement.

L’axiomatique

La formalisation conduit naturellement Peano à exposer la mathématique sous forme axiomatique. On trouvera à l’article AXIOMATIQUE la description des principales contributions de Peano dans ce domaine. Indépendamment de R. Dedekind, il formule les axiomes de Peano relatifs aux nombres entiers naturels. C’est également lui qui a énoncé pour la première fois, en 1888, les axiomes des espaces vectoriels sur le corps R, sans restriction de dimension. Il entrevoit l’importance de l’algèbre linéaire et dégage la notion d’application linéaire sous une forme toute moderne. Il explicite les liens qui existent entre les espaces vectoriels, affines et euclidiens. D’autre part, Peano a été l’avocat ardent des efforts de M. Pasch et D. Hilbert pour élaborer l’axiomatisation de la géométrie élémentaire.

Mathématiques appliquées

Le travail d’abstraction progressive entrepris par Peano s’accompagne constamment d’une réflexion concernant les problèmes pratiques. Sa contribution à l’analyse numérique est importante: il a perfectionné notamment les techniques d’interpolation et de quadrature approchée, et, surtout, il a mis en évidence la structure des restes des formules de l’analyse numérique. D’après Peano, le reste d’une formule qui est exacte pour les fonctions polynomiales de degré n s’exprime sous forme intégrale à l’aide d’un noyau qui est une fonction polynomiale par morceaux.

En mécanique rationnelle, il a contribué à faire adopter des notations intrinsèques. On lui doit l’explication du déplacement du pôle sur le globe terrestre. Il a également éclairci le «paradoxe de la chute du chat», qui occupa la mémorable séance du 29 octobre 1894 à l’Académie des sciences de Paris: il s’agissait de comprendre comment, si l’on fait tomber, en chute libre, un chat avec les quatre pattes en l’air, l’animal retombait toujours sur ses pieds.

L’érudition de Peano dans le domaine de l’histoire des mathématiques est considérable. Rejetant les détails anecdotiques, il s’intéresse essentiellement à la genèse des idées: c’est ce même point de vue qui sera repris par N. Bourbaki.

L’intérêt de Peano pour les questions sociales est attesté par son projet de caisse mutuelle coopérative de retraite, dont il a élaboré la théorie mathématique, et par son activité à la tête du mouvement Interlingua pour le rapprochement des peuples.

Ce savant sort des sentiers battus dans tous les domaines, anticipant sur des modes futures. Ainsi, dès 1912, il prend vigoureusement position contre l’institution des examens dans les universités! Il s’insurge de devoir être simultanément un père et un juge pour ses élèves, ce qui les incite à l’aimer comme un père et à le détester en tant que juge.

Encyclopédie Universelle. 2012.